Towards Physics-informed Deep Learning for Turbulent Flow Prediction
Prediction Visualization
We propose a novel hybrid model for turbulence prediction, $\texttt{TF-Net}$, that unifies a popular Computational fluid dynamics (CFD) technique, RANS-LES coupling, with custom-designed U-net. The following two videos show the ground truth and the predicted U (left) and V (right) velocity fields from $\texttt{TF-Net}$ and three best baselines. We see that the predictions by $\texttt{TF-Net}$ are the closest to the target based on the shape and the frequency of the motions. Baselines generate smooth predictions and miss the details of small scale motion.
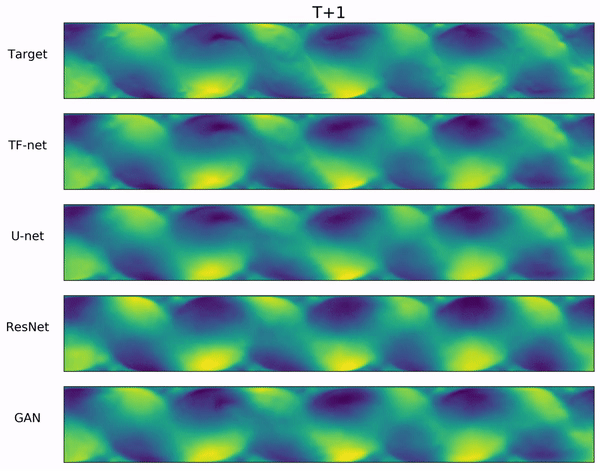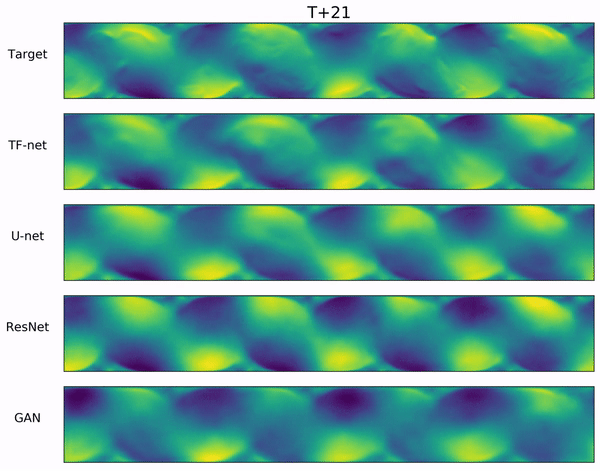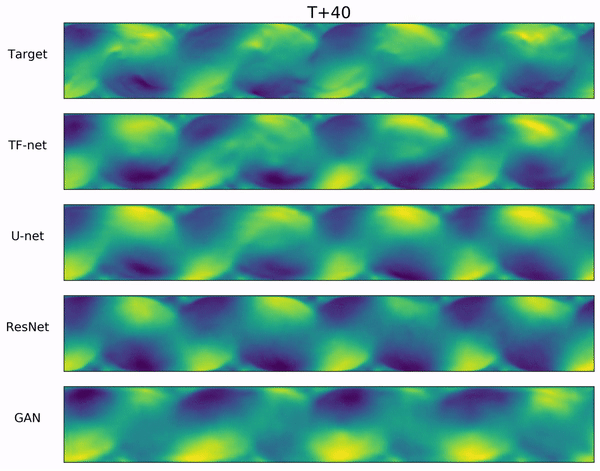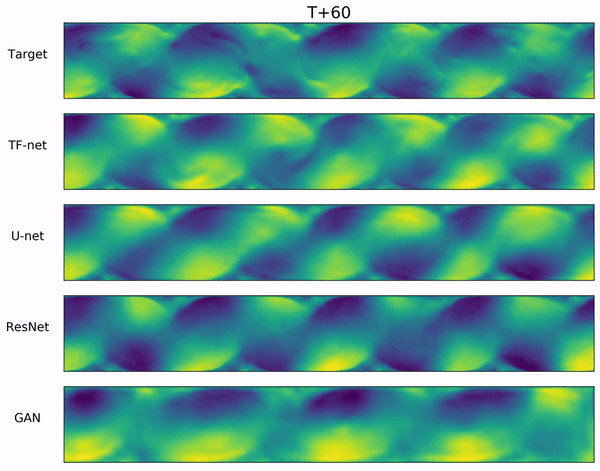
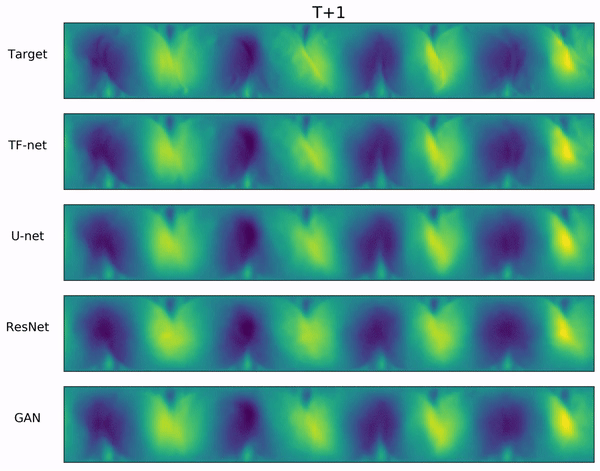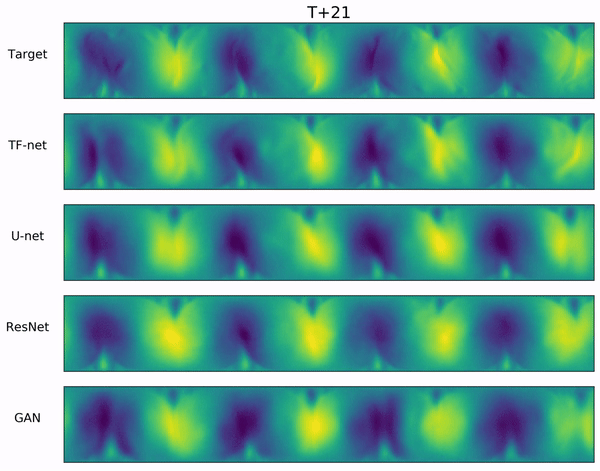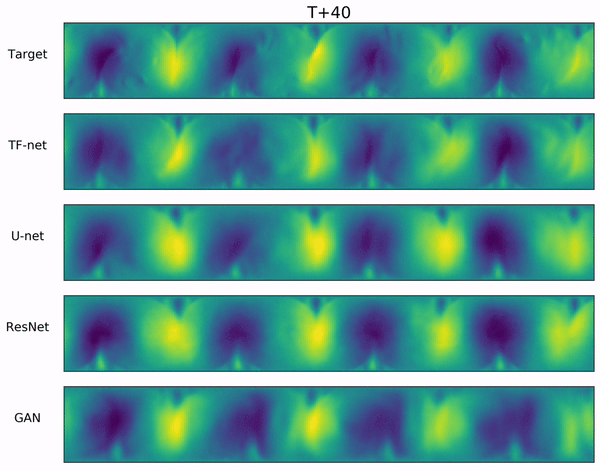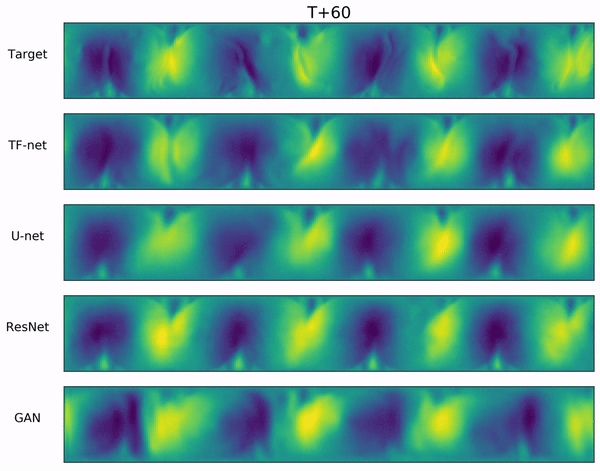
Introduction
Modeling the spatiotemporal dynamics over a wide range of space and time scales is a fundamental task in science, especially atmospheric science, marine science and aerodynamics. Computational fluid dynamics (CFD) is at the heart of climate modeling and has direct implications for understanding and predicting climate change. Recently, deep learning have demonstrated great success in the automation, acceleration, and streamlining of highly compute-intensive workflows for science. We hope deep learning can accelerate the turbulence simulation since the current CFD is purely physics-based and computationally-intensive, requiring significant computational resources and expertise.

But purely data-driven methods are mainly statistical with no underlying physical knowledge incorporated, and are yet to be proven to be successful in capturing and predicting accurately the complex physical systems. Incorporating physics knowledge into deep learning models can improve not only prediction accuracy, but more importantly, physical consistency. Thus, developing deep learning methods that can incorporate physical laws in a systematic manner is a key element in advancing AI for physical sciences.
Computational techniques are at the core of present-day turbulence investigations, which are a branch of fluid mechanics that uses numerical method to analyze and predict fluid flows. In physics, people use the following Navier–Stokes equations to describe the motion of viscous fluid dynamics.
\[\nabla \cdot \pmb{w} = 0 \qquad\qquad\qquad\qquad\qquad\qquad\qquad \text{Continuity Equation}\] \[\frac{\partial \pmb{w}}{\partial t} + (\pmb{w} \cdot \nabla) \pmb{w} = -\frac{1}{\rho_0} \nabla p + \nu \nabla^2 \pmb{w} + f \quad\text{Momentum Equation}\] \[\frac{\partial T}{\partial t} + (\pmb{w} \cdot \nabla) T = \kappa \nabla^2 T \qquad\qquad\qquad\quad \text{Temperature Equation}\]where $\pmb{w}(t)$ is the vector velocity field of the flow, which is what we want to predict. $p$ and $T$ are pressure and temperature respectively, $\kappa$ is the coefficient of heat conductivity, $\rho_0$ is density at temperature at the beginning, $\alpha$ is the coefficient of thermal expansion, $\nu$ is the kinematic viscosity, $f$ the body force that is due to gravity.
Turbulent-Flow Net
For turbulent flows, the range of length scales and complexity of phenomena involved in turbulence make Direct Numerical Simulation (DNS) approaches prohibitively expensive. Great emphasis was then placed on the alternative approaches including Large-Eddy Simulation (LES), Reynolds-averaged Navier Stokes (RANS) as well as Hybrid RANS-LES Coupling that combines both RANS and LES approaches in order to take advantage of both methods. These methods decompose the fluid flow into different scales in order to directly simulate large scales while model small ones.
Hybrid RANS-LES Coupling decomposes the flow velocity into three scales: mean flow, resolved fluctuations and unresolved fluctuations. It applies the spatial filtering operator $S$ and the temporal average operator $T$ sequentially.
\[\pmb{w^*}(\pmb{x},t) = S \ast\pmb{w} = \sum_{\pmb{\xi}} S(\pmb{x}|\pmb{\xi})\pmb{w}(\pmb{\xi},t)\] \[\pmb{\bar{w}}(\pmb{x},t) = T \ast \pmb{w^*} = \frac{1}{n}\sum_{s = t-n}^tT(s) \pmb{w^*} (\pmb{x}, s)\]then $\pmb{\tilde{w}}$ can be defined as the difference between $\pmb{w^*}$ and $\pmb{\bar{w}}$:
\[\pmb{\tilde{w}} = \pmb{w^*} - \pmb{\bar{w}}, \quad \pmb{w'} = \pmb{w} - \pmb{w^{*}}\]Finally we can have the three-level decomposition of the velocity field.
\begin{equation} \pmb{w} = \pmb{\bar{w}} + \pmb{\tilde{w}} + \pmb{w’} \end{equation}
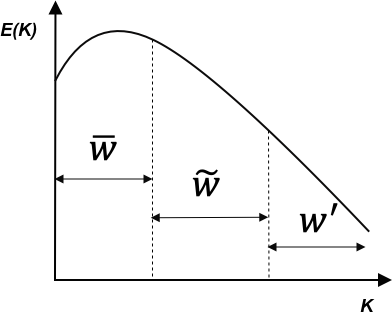
The figure below shows this three-level decomposition in wavenumber space. $k$ is the wavenumber, the spatial frequency in the Fourier domain. $E(k)$ is the energy spectrum describing how much kinetic energy is contained in eddies with wavenumber $k$. Small $k$ corresponds to large eddies that contain most of the energy. The slope of the spectrum is negative and indicates the transfer of energy from large scales of motion to the small scales.
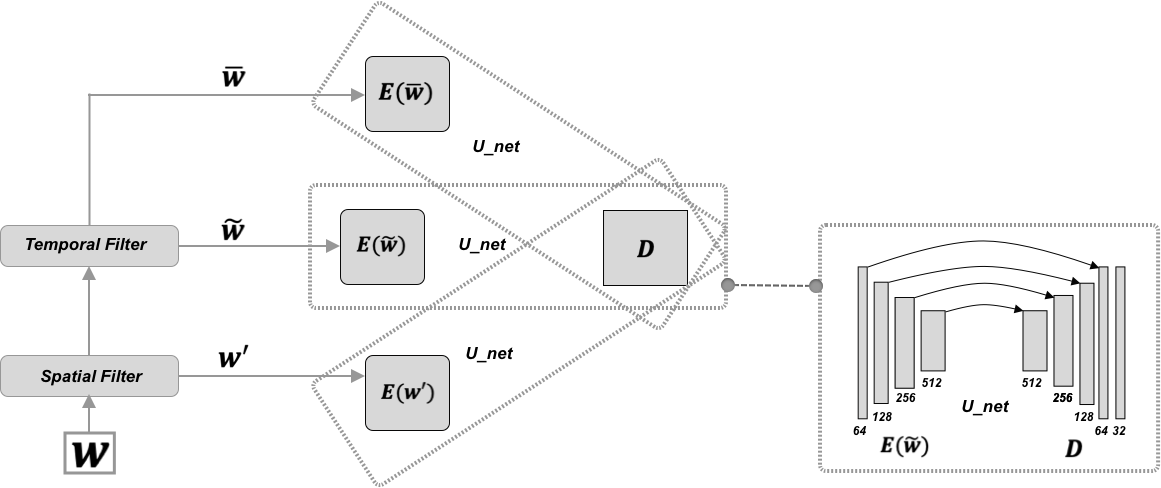
Inspired by the hybrid RANS-LES Coupling, we propose a hybrid deep learning framework, $\texttt{TF-Net}$, based on the multilevel spectral decomposition. Specifically, we decompose the velocity field into three scales using the spatial filter $S$ and the temporal filter $T$. Unlike traditional CFD, both filters in $\texttt{TF-Net}$ are trainable neural networks. The motivation for this design is to explicitly guide the DL model to learn the non-linear dynamics of both large and small eddies. We design three identical convolutional encoders to encode the three scale components separately and use a shared convolutional decoder to learn the interactions among these three components and generate the final prediction. The figure below shows the overall architecture of our hybrid model $\texttt{TF-Net}$.
Since the turbulent flow under investigation has zero divergence, we include $\Vert\nabla \cdot \pmb{w}\Vert^2$ as a regularizer to constrain the predictions, leading to a constrained TF-Net, $\texttt{Con TF-Net}$.
Results
We compare our model with four purely data-driven deep learning models, including $\texttt{ResNet}$, $\texttt{ConvLSTM}$, $\texttt{U-net}$ and $\texttt{GAN}$, and two hybrid physics-informed models, including $\texttt{DHPM}$ and $\texttt{SST}$. All the models trained to make one step ahead prediction given the historic frames and we use them autoregressively to generate multi-step forecasts.
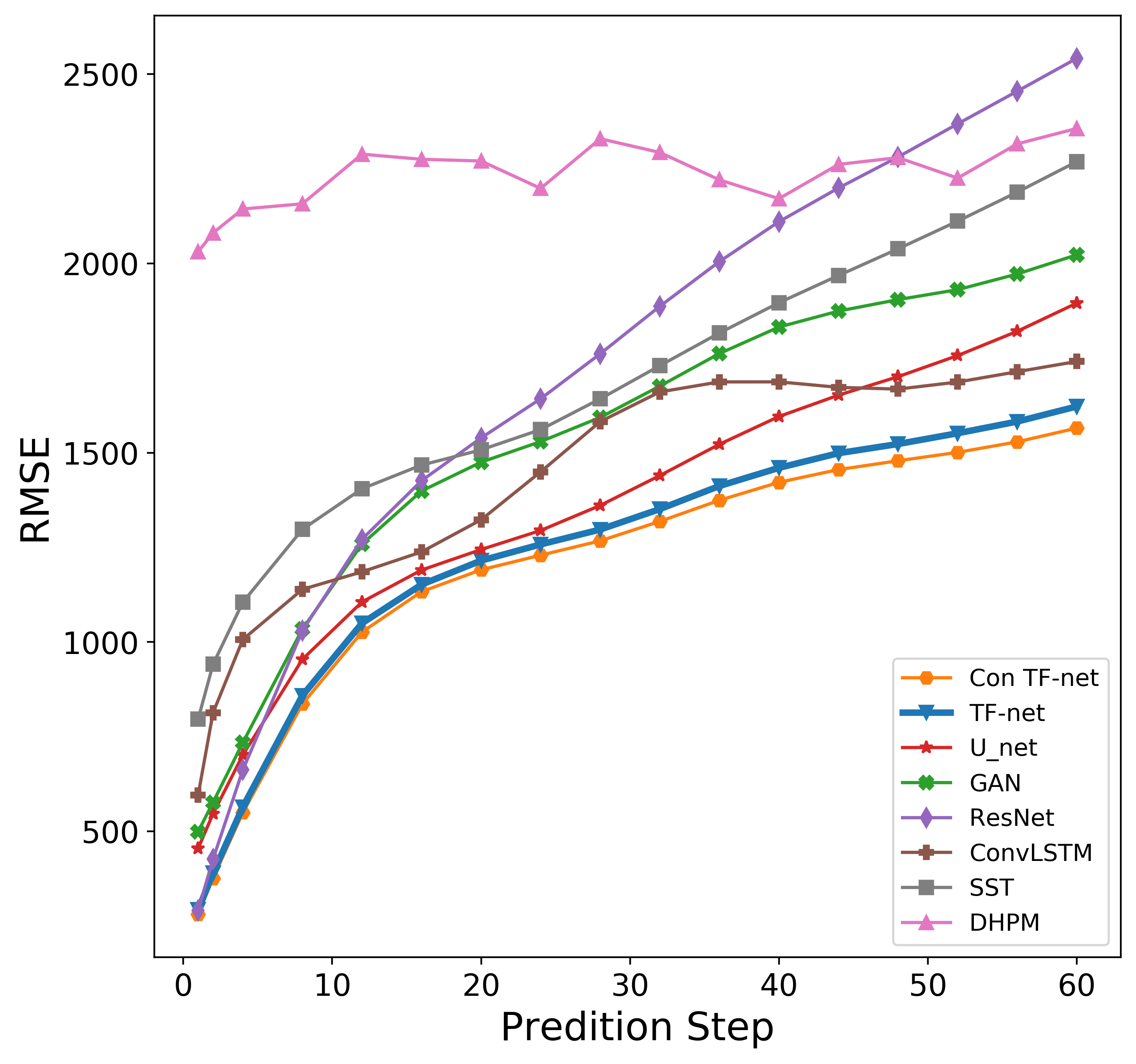
$\textbf{Accuracy}$ The following figure show the growth of RMSE with prediction horizon up to 60 time steps ahead. We can see that $\texttt{TF-Net}$ consistently outperforms all baselines, and constraining it with divergence free regularizer can further improve the performance.
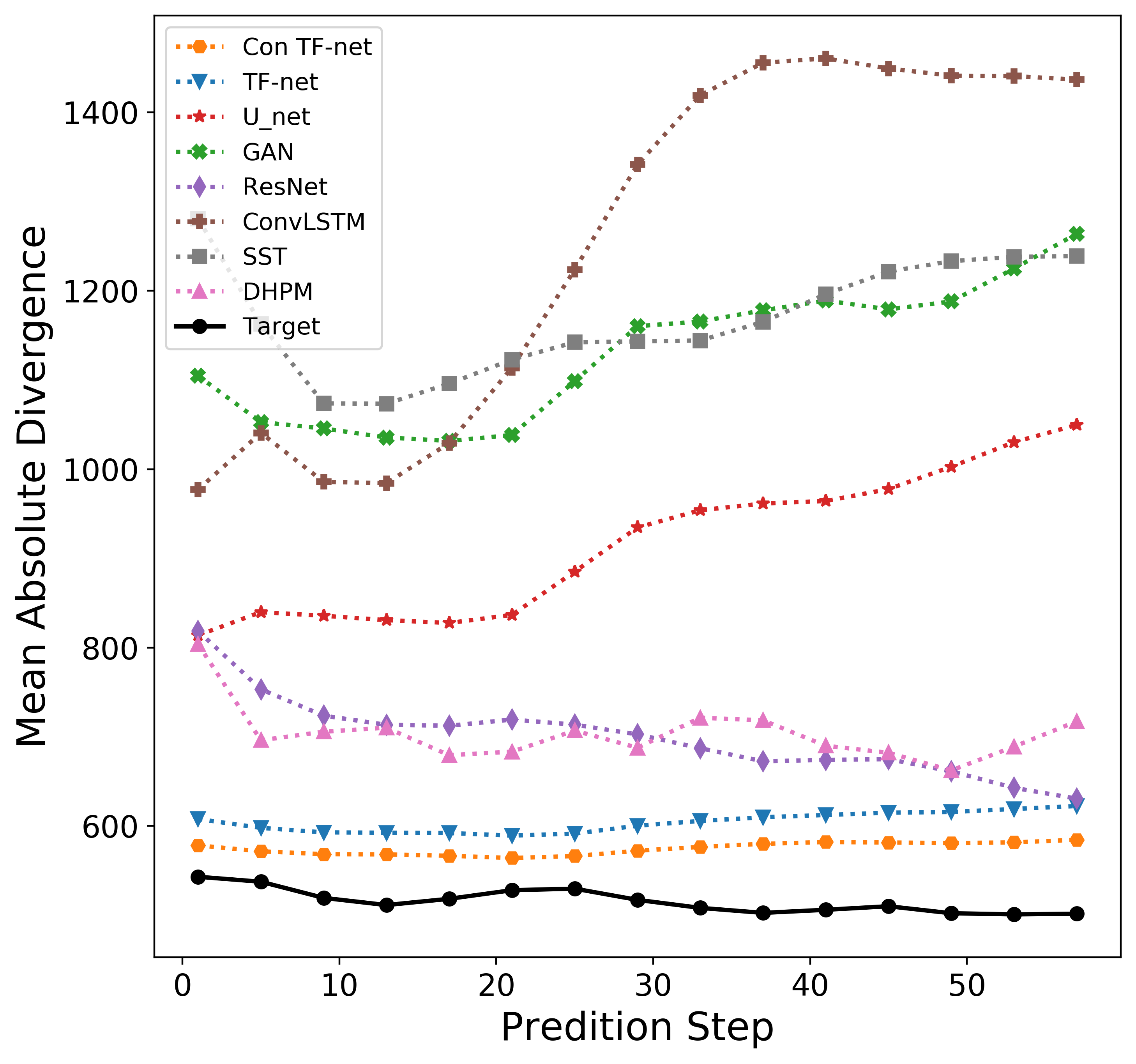
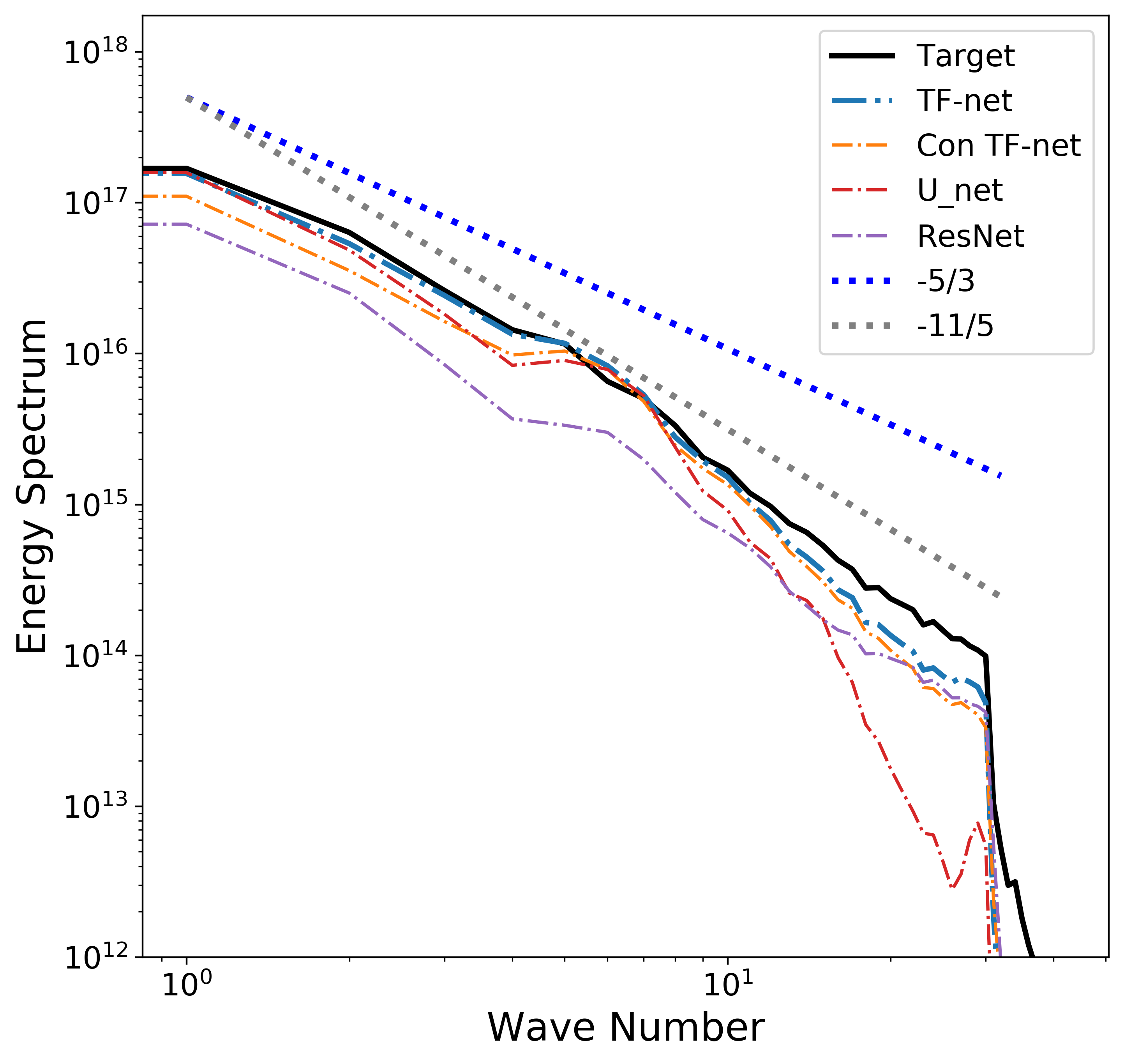
$\textbf{Physical Consistency}$ The left figure below is the averages of absolute divergence over all pixels at each prediction step and the right figure below is the energy spectrum curves. $\texttt{TF-Net}$ predictions are in fact much closer to the target even without additional divergence free constraint, which suggests that $\texttt{TF-Net}$ can generate predictions that are physically consistent with the ground truth.
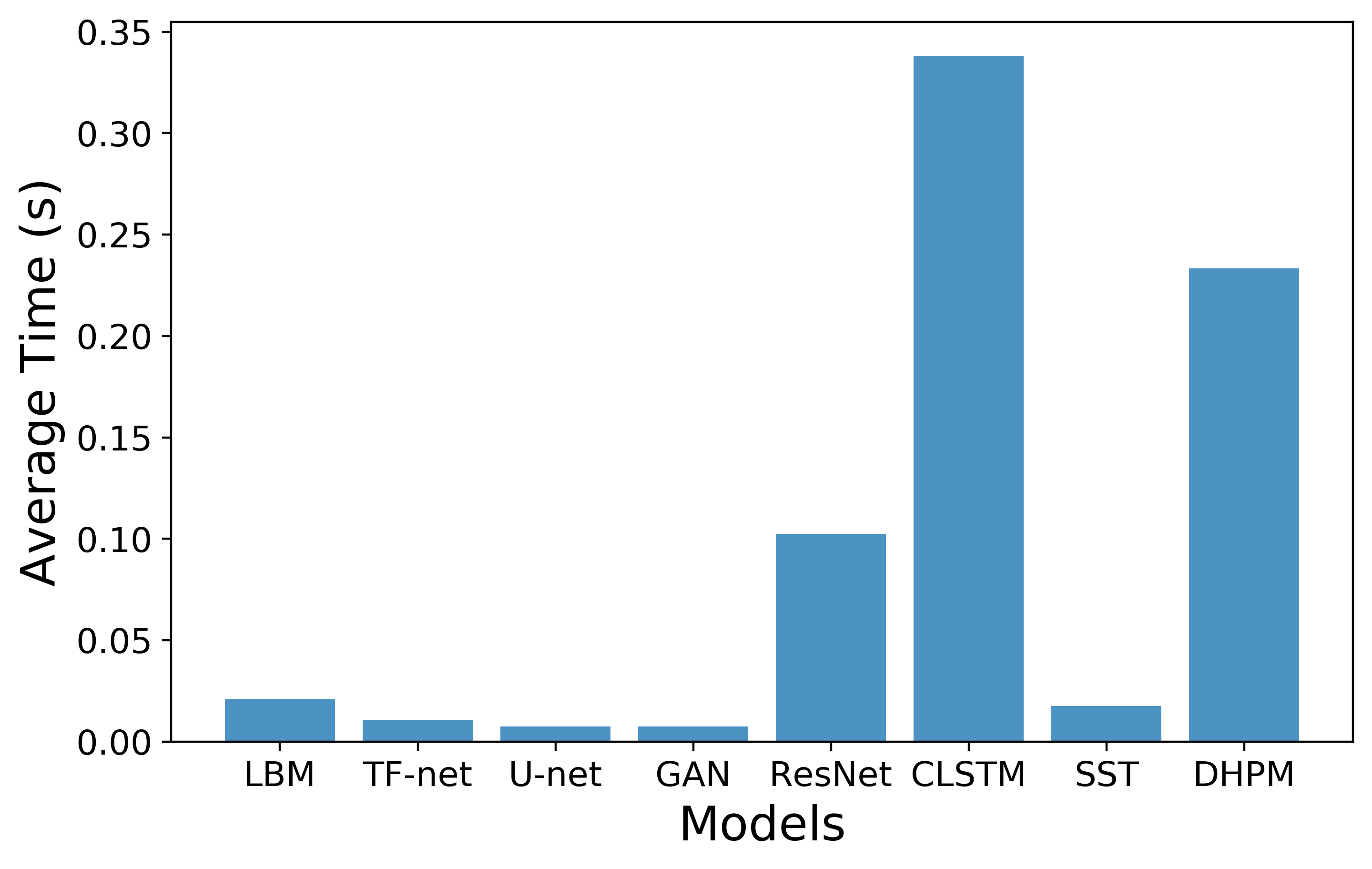
$\textbf{Efficiency}$ This figure shows the average time to produce one 64 × 448 2d velocity field for all models on single V100 GPU. We can see that $\texttt{TF-net}$, $\texttt{U_net}$ and $\texttt{GAN}$ are faster than the numerical Lattice Boltzmann method. $\texttt{TF-Net}$ will show greater advantage of speed on higher resolution data.
$\textbf{Ablation Study}$ We also perform an ablation study to understand each component of $\texttt{TF-Net}$ and investigate whether the model has actually learned the flow with different scales. During inference, we applied each small U-net in $\texttt{TF-Net}$ with the other two encoders removed to the entire input domain. The video below includes $\texttt{TF-Net}$ predictions and the outputs of each small $\texttt{U-net}$ while the other two encoders are zeroed out. We observe that the outputs of each small $\texttt{U-net}$ are the flow with different scales, which demonstrates that $\texttt{TF-Net}$ can learn multi-scale behaviors.
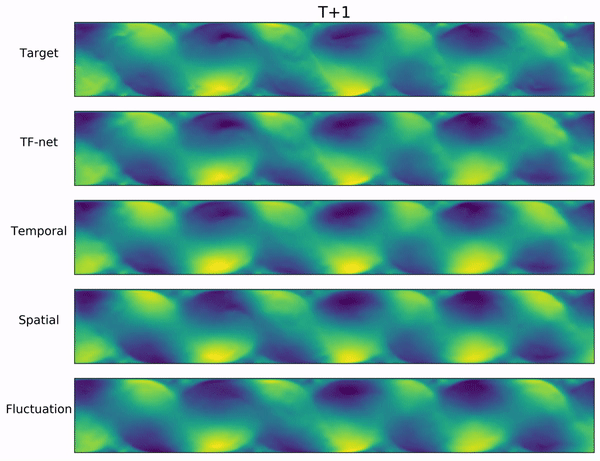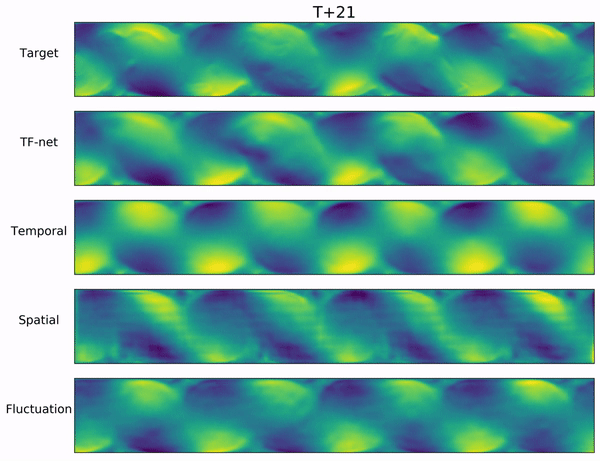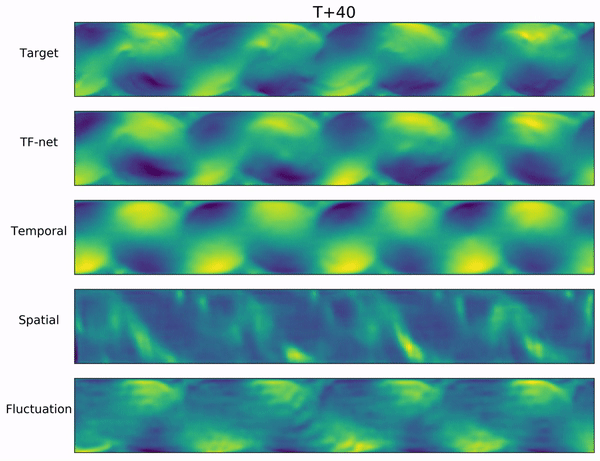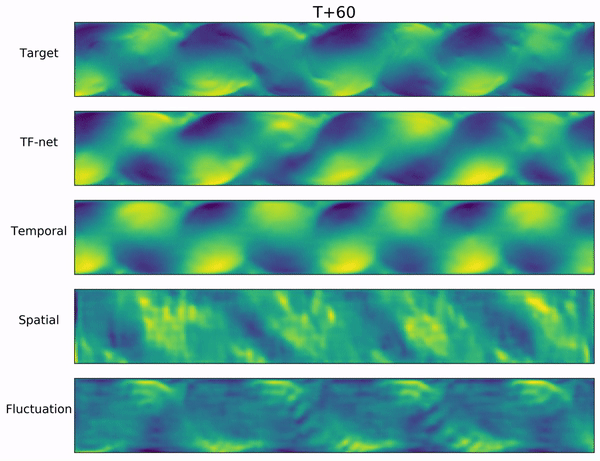
Conclusion and Future Work
We presented a novel hybrid deep learning model, $\texttt{TF-Net}$, that unifies representation learning and turbulence simulation techniques. $\texttt{TF-Net}$ exploits the multi-scale behavior of turbulent flows to design trainable scale-separation operators to model different ranges of scales individually. We provide exhaustive comparisons of $\texttt{TF-Net}$ and baselines and observe significant improvement in both the prediction error and desired physical quantifies, including divergence, turbulence kinetic energy and energy spectrum. Future work includes extending these techniques to very high-resolution, 3D turbulent flows and incorporating additional physical variables, such as pressure and temperature, and additional physical constraints, such as conservation of momentum, to improve the accuracy and faithfulness of deep learning models.