FairProof : Confidential and Certifiable Fairness for Neural Networks
Machine learning models are increasingly used in societal applications, yet legal and privacy concerns demand that they very often be kept confidential. Consequently, there is a growing distrust about the fairness properties of these models in the minds of consumers, who are often at the receiving end of model predictions. To this end, we propose FairProof -- a system that uses Zero-Knowledge Proofs (a cryptographic primitive) to publicly verify the fairness of a model, while maintaining confidentiality. We also propose a fairness certification algorithm for fully-connected neural networks which is befitting to ZKPs and is used in this system. We implement FairProof in Gnark and demonstrate empirically that our system is practically feasible. Code is available at [https://github.com/infinite-pursuits/FairProof](https://github.com/infinite-pursuits/FairProof).
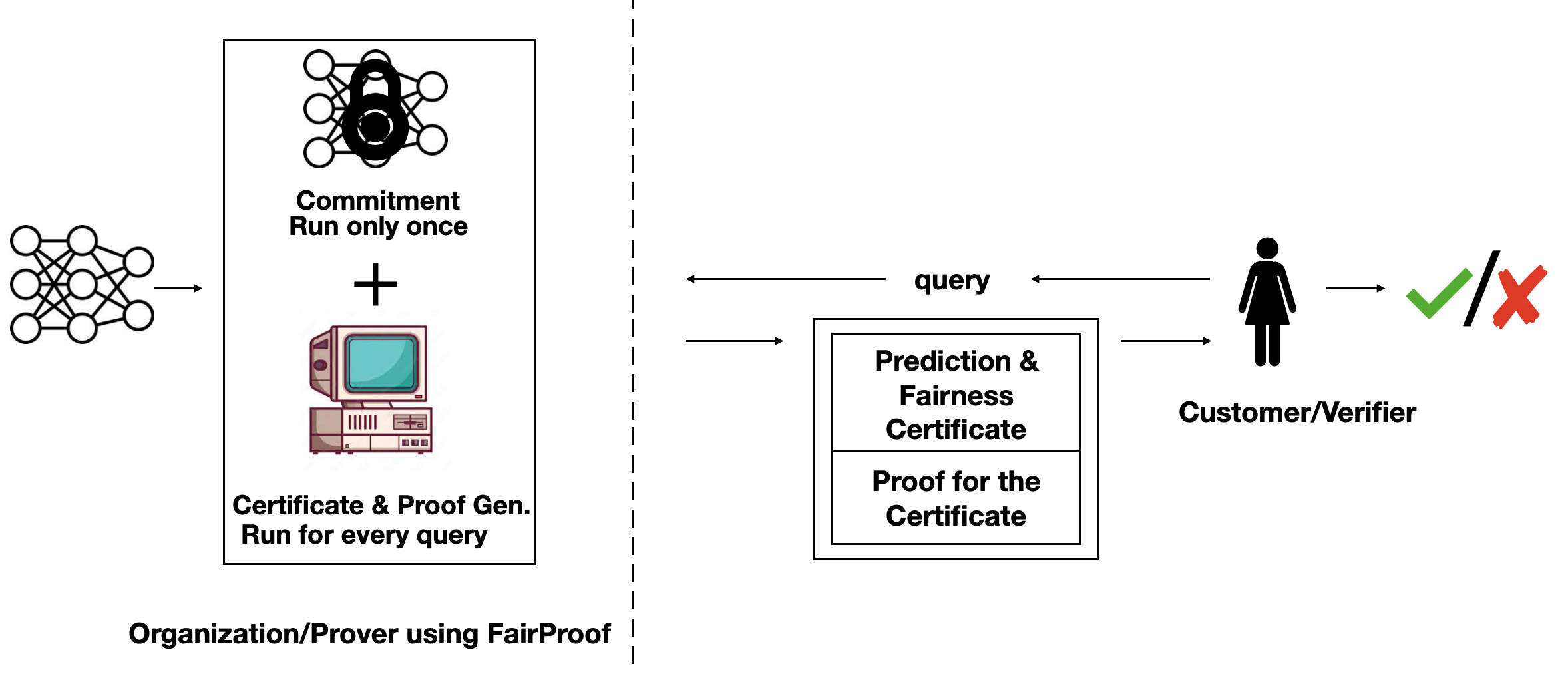
Introduction
As machine learning models proliferate in societal applications , it is important to verify that they possess desirable properties such as accuracy, fairness and privacy. Additionally due to legal and IP reasons, models are kept confidential and therefore verification techniques should respect this confidentiality. This brings us to the question of how do we verify properties of a model while maintaining confidentiality.
The canonical approach to verification is ‘third-party auditing’
Our Key Idea
Motivated by these issues, we propose an alternate framework for verification which is based on Zero-Knowledge Proofs (ZKPs)
Guarantees of FairProof
In this work, we propose a ZKP system called FairProof to verify the fairness of a model. We want FairProof to give the following three guarantees: 1) ensure that the same model is used for all customers, 2) maintain the confidentiality of the model and 3) the fairness score is correctly computed without manipulation using the fixed model weights only. The first requirement is guaranteed through model commitments – a cryptographic commitment to the model weights binds the organization to those weights publicly while maintaining confidentiality of the weights and has been widely studied in the ML security literature
Problem Setting
Consider the following problem setting: on one hand, we have a customer which applies for a loan (i.e. query) and corresponds to the verifier while on the other, we have a bank which uses a machine learning model to make loan decisions and corresponds to the prover. Along with the loan decision, the bank also gives a fairness certificate and a cryptographic proof proving the correct computation of this certificate. The verifier verifies this proof without looking at the model weights.
Two parts of FairProof
There are two important parts to FairProof : 1) How to calculate the fairness certificate (in-the-clear)? and 2) How to verify this certificate with ZKPs?
Fairness Certification in-the-clear
The fairness metric we use is Local Individual Fairness (IF) and give a simple algorithm to calculate this certificate by using a connection between adversarial robustness and IF. Experimentally, we see that the resulting certification algorithm is able to differentiate between less and more fair models.
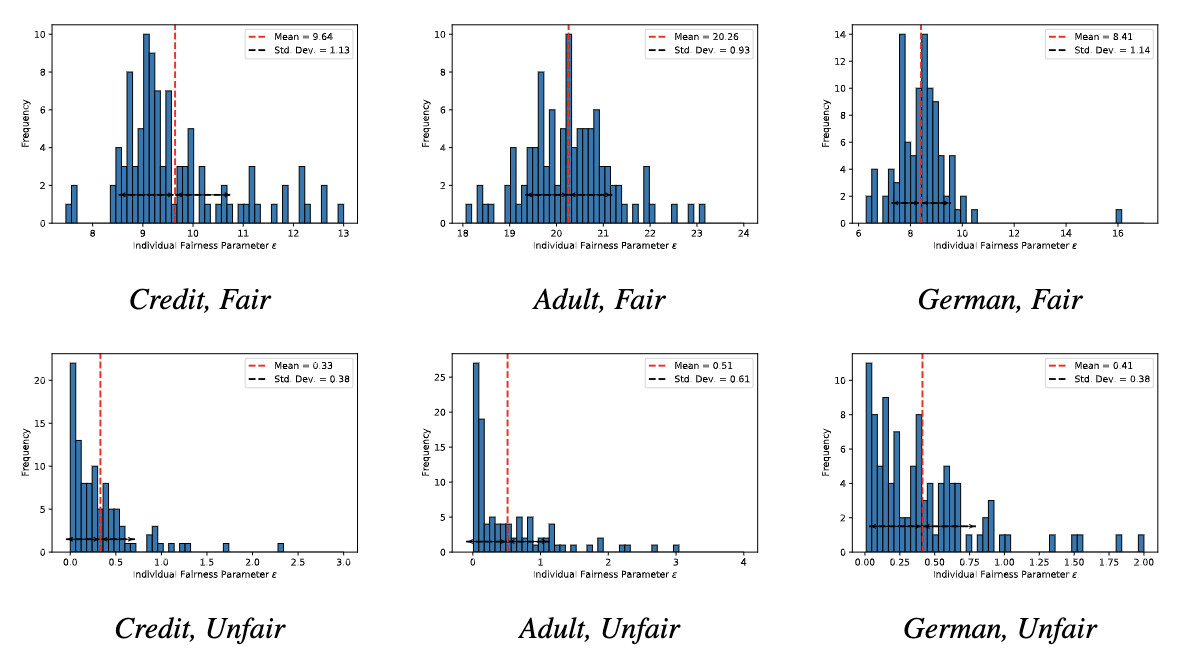
ZKP for Fairness Certification
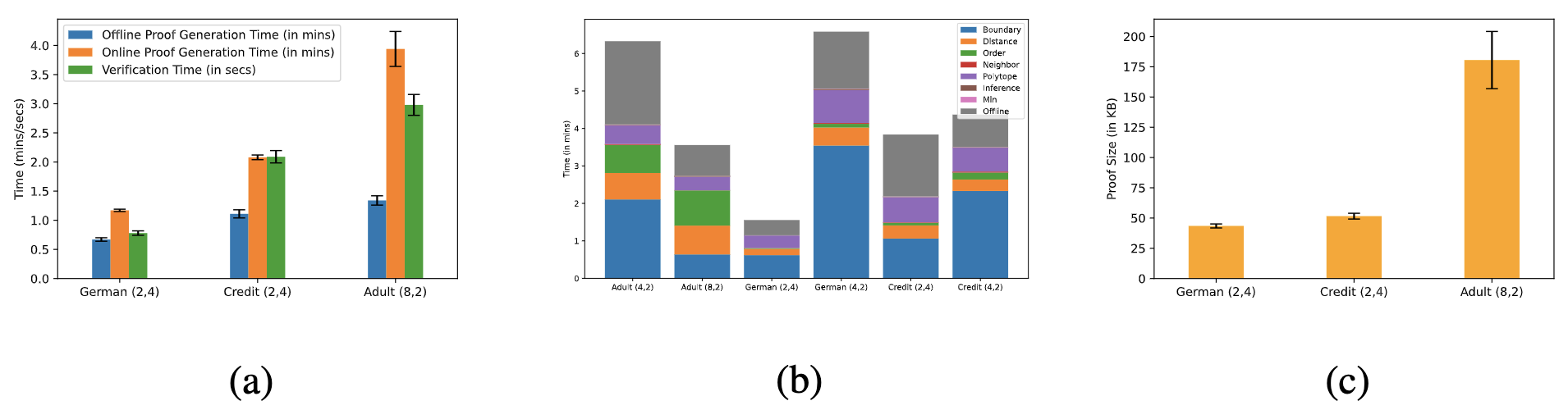
Next we must code this certification algorithm in a ZKP library. However, ZKPs are infamous for adding a big computational overhead and can be notoriously hard to code due to only using arithmetic operations. To overcome these challenges, we strategically choose some sub-functionalities which are enough to verify the certificate and also propose to do some computations offline to save time.
Empirically we find that the maximum proof generation time is on ~4 min while the maximum verification time is ~3 seconds (note the change from minutes to seconds). Maximum time is consumed by the VerifyNeighbor functionality. Also the proof size is a meagre 200 KB.
Conclusion
In conclusion, we propose FairProof – a protocol enabling model owners to issue publicly verifiable certificates while ensuring model confidentiality. While our work is grounded in fairness and societal applications, we believe that ZKPs are a general-purpose tool and can be a promising solution for overcoming problems arising out of the need for model confidentiality in other areas/applications as well.
For code check this link : https://github.com/infinite-pursuits/FairProof
For the paper check this link : https://arxiv.org/pdf/2402.12572
For any enquiries, write to : cyadav@ucsd.edu